Факториал в Excel
В этой статье я расскажу о факториале, его свойствах и о том, как вычислить его значение с помощью Excel. Мы проверим, как точно вычисляет значение факториала формула Стирлинга и разберем решение типовых задач с факториалами, а на закуску - несколько видеороликов (и конечно расчетный файл эксель). Удачи!
Что такое факториал?
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. Факториал определен только для целых неотрицательных чисел.
$$n!=1\cdot 2\cdot 3 \cdot ... \cdot (n-1) \cdot n$$По определению, считают, что $0!=1, 1!=1$. Далее:
$$ 2!=1 \cdot 2 = 2,\\ 3!=1 \cdot 2 \cdot 3= 6,\\ 4!=1 \cdot 2 \cdot 3\cdot 4= 24,\\ 5!=1 \cdot 2 \cdot 3\cdot 4\cdot 5= 120,\\ ... $$Факториал растет невероятно быстро (недаром он обозначается восклицательным знаком!), существенно быстрее степенной $x^n$ или даже экспоненциальной функции $e^n$ (но медленее чем $e^{e^n}$)
Факториал широко применяется в комбинаторике - он равен числу всех перестановок $n$-элементного множества, а также входит в формулы для числа сочетаний и размещений. Факториал встречается в математическом анализе (чаще при разложениях функции в степенные ряды), а также в функциональном анализе и теории чисел.
Еще: онлайн калькулятор факториала.
Формулы и свойства факториала
Рекуррентная формула для факториала:
$$ n!=\left\{ \begin{matrix} 1, & n=0,\\ (n-1)!\cdot n, & n \gt 0.\\ \end{matrix} \right. $$Факториал связан с гамма-функцией по формуле: $n!= \Gamma(n+1)$. Фактически, гамма-функция - обобщение понятия факториала на все положительные вещственные функции.
Для любого натурального $n$ выполняется:
$$ (n!)^2 \ge n^n \ge n! \ge n. $$Любопытная формула связывает факториал и производную степенной функции:
$$ (x^n)^{(n)} = n!$$Формула Стирлинга
Для приближенного вычисления факториала применяют асимптотическую формулу Стирлинга:
$$ n!=\sqrt{2\pi n} \left( \frac{n}{e}\right )^n \left(1+ \frac{1}{12n}+ \frac{1}{288n^2}- \frac{139}{51840n^3}- \frac{571}{2488320n^4}+... \right ) $$Обычно для расчетов берут только главный член:
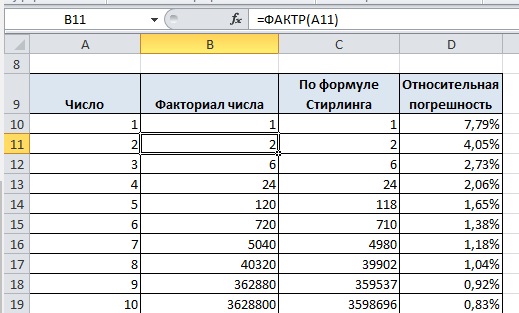
$$ n! \approx \sqrt{2\pi n} \left( \frac{n}{e}\right )^n. $$Ниже вы увидите пример расчета факториала по обычной формуле и с помощью формулы Стирлинга, которая, как видно, дает вполне хорошее приближение (начиная с $n=9$ относительная погрешность уже меньше 1%).
Расчет факториала в Эксель
Для нахождения факториала в Excel нужно использовать специальную функцию =ФАКТР($n$), где $n$ - число, факториал которого нужно найти.
Пример расчета и ввода формулы ниже на скриншоте, также вы можете скачать расчетный файл
Примеры задач с факториалом
Рассмотрим решение типовых задач.
Пример 1. На полке стоят 8 дисков. Сколькими способами их можно расставить между собой?
Решение. Требуется найти число всех перестановок 8 различных объектов, что вычисляется как раз как факториал:
$$N=8!=1 \cdot 2 \cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot 8=40320.$$Пример 2. Вычислить
$$ \frac{60!}{58!}-\frac{6!}{5!} $$Решение.
$$ \frac{60!}{58!}-\frac{6!}{5!}=\frac{58!\cdot 59\cdot 60}{58!}-\frac{5! \cdot 6}{5!}=59\cdot 60-6=3534. $$Пример 3. Упростить выражение
$$ \frac{n+3}{(n+1)!}-\frac{1}{n!} $$Решение.
$$ \frac{n+3}{(n+1)!}-\frac{1}{n!} = \frac{n+3}{(n+1)!}-\frac{n+1}{n!(n+1)}=\frac{n+3-(n+1)}{(n+1)!}= \frac{2}{(n+1)!} $$Пример 4. Упростить дробь, содержащую факториал:
$$ \frac{n!}{(n-2)!} $$Решение.
$$ \frac{n!}{(n-2)!}=\frac{ (n-1)! \cdot n}{(n-2)!} =\frac{(n-2)! \cdot (n-1) \cdot n}{(n-2)!} = (n-1) \cdot n = n^2-n$$Видео о факториале
Небольшое учебное видео про факториал - определение, свойства, как быстро растет, как вычислить в Excel по встроенной формуле и по приближенной формуле Стирлинга.
Расчетный файл из видео можно скачать
Напоследок - насколько быстро растет факториал!




